Performance proportionality is one of the key requirements for a dynamic tracing system. In practice though, its a requirement that’s pretty difficult to satisfy. As with most non-functional requirements, performance proportionality is actually a pretty mushy and subjective concept.

Experimentation performed with Google’s Dapper system showed that tracing all of the Web search cluster’s RPCs increased response latency by 16.3% (whilst throughput reduced by a relatively modest 1.48%). Though these costs may indeed be proportional, the system’s developers were unwilling to accept them. Thus, what we’re really aiming for is that tracing stays under the radar of anyone with the power to disable it.

In their paper So you want to trace your distributed system?, Sambasivan et al. identify random sampling as key to reducing overheads imposed by a distributed tracing. Using Dapper to trace Web search RPCs with a uniform at a sampling rate of 1/1024 significantly reduces overheads, with the response latency measured at a mere 0.20% over the baseline system (and throughput reduced by 0.06%). Provided the system being traced experiences a high volume of requests, sampling at this rate is still sufficient to diagnose even rare performance issues.

Note: Dapper’s sampling scheme is head-based, that is, the sampling decision is taken once at the start of the trace.

rand()

Random sampling of DTrace probes can be easily achieved by specifying a predicate that is conditional on the output of the rand() subroutine:

Name	Prototype	Description
rand	int rand (void)	Returns a pseudo-random integer.

For example, using the tick-1s probe we can sample at 0.5 and 0.25s intervals:

tick-1s
/rand()%2 == 0/
{
   @time["sample"] = quantize(2);
}

tick-1s
/rand()%4 == 0/
{
   @time["sample"] = quantize(4);
}


rand() distribution

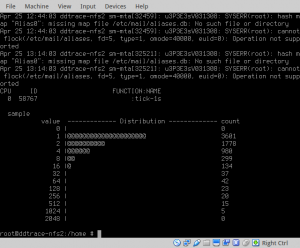
Expanding on the approach shown above we can generate and visualize rand()‘s sampling distribution (the figure below, shows DTrace’s rand() sampling distribution captured over the period of an hour):

Sampling at 1/2 second (rand()&2 == 0) and 1/4 second (rand()%4 == 0) intervals give values close to what we’d expect (1778 and 980 compared to expected values of 1800 and 900). However, at 1/8 second there is a significantly lower number of samples than the expected value; 299 compared to the expected value of 450 (this is also true of the value at 1/16 second, 134 compared to an expected value of 225). Clearly the output of rand() is non-uniform (and wouldn’t pass tests for statistical randomness). Delving into rand()‘s implementation the reasons for non-uniformity in the output are apparent.

Implementation

rand() is implemented as a Linear Congruential Generator (LGC). An LCG is an algorithm for producing a sequence of pseudo-randomized numbers calculated with a discontinuous piecewise linear equation. The main advantages of LCGs are that they are fast and require minimal amounts of state. However, LCGs also have disadvantages. Notable they exhibit biases, that is, the probability of each bit in the output is non-uniform.

DTrace’s implementation of rand() is shown below. The LGC’s parameters a = 2416, c = 374441 and m = 1771875 give a maximal sequence of 1771875 pseudo-random values.

sys/cddl/contrib/opensolaris/uts/common/dtrace/dtrace.c

case DIF_SUBR_RAND:
   regs[rd] = (dtrace_gethrtime() * 2416 + 374441) % 1771875;
   break;


LCG’s require maintaining minimal amounts of state (typically 32 or 64bits). DTrace’s implementation goes one better and maintains zero state. Each invocation of rand(), (re)seeds the LCG by calling dtrace_gethrtime() (the time in ns since system reset). Removing shared mutable state is highly desirable as, in order to guarantee production safety, it is forbidden to hold locks whislt executing in the context of a DTrace probe.

dtrace_gethrtime() reads its value from the hardware TSC (Time Stamp Counter). Thus the time return by this function is synchronized across the CPU’s cores. As the pseudo-random sequence is shared by all the CPU cores and the time is synchronized across the cores, it is possible for two independent probes to read the same output from rand(). This isn’t disastrous. However, together with the other weaknesses its yucky enough to suggest that we might be benefit from an alternative way of generating pseudo-randomness.

To recap DTrace’s rand() implementation has (arguably) a number of weaknesses that make it less than suitable for uniform random sampling of high-volume, online services (such as Web search):

• Significant and detectable biases in its output bits.
• All CPU cores share the same sequence (and can even return the exact same value).
• Relatively small sequence (1771875 values).

random()

Requirements

The main requirements generating randomness for distributed tracing are:

• Output passes tests for statistical randomness.
• Large (very large?) sequence space.
• Non-overlapping sequences per CPU core.
• Performance closely matching (or exceeding) that of an LCG.

Cryptographically strong randomness is a non-requirement (even if it weren’t blocking on the entropy device is a no no in a DTrace probe context).

Implementation

The requirements for generating randomness closely match the xorshift class of pseudo-random number generators. xorshift generators output the next number in their sequence by repeatedly taking the exclusive or of a number with a bit-shifted version of itself [1]. As an example, the xorshift128+ generator generates a high-quality 64-bit value very quickly with a maximal sequence of 2^128-1 values. xorshift128+ is presently used in the JavaScript engines of Chrome, Firefox and Safari, and it is the default generator in Erlang [2].

For this work I have opted for the xoroshiro128+ generator:

xoroshiro128+ (XOR/rotate/shift/rotate) is the successor to xorshift128+. Instead of perpetuating Marsaglia’s tradition of xorshift as a basic operation, xoroshiro128+ uses a carefully handcrafted shift/rotate-based linear transformation designed in collaboration with David Blackman. The result is a significant improvement in speed (well below a nanosecond per integer) and a significant improvement in statistical quality, as detected by the long-range tests of PractRand. xoroshiro128+ is our current suggestion for replacing low-quality generators commonly found in programming languages. [2]

Seeding

On initialisation of the dtrace kernel module, the new DTrace pseudo-random number generator is seeded with 128bits of entropy gathered from the system’s entropy device (/dev/fortuna).
sys/cddl/contrib/opensolaris/uts/common/dtrace/dtrace.c

(void) read_random(&state->dts_rstate[0], 2 * sizeof(uint64_t));


Where, dts_rstate is a two-dimensional array for storing per-CPU core random state.
sys/cddl/contrib/opensolaris/uts/common/sys/dtrace_impl.c

struct dtrace_state {
   ...
   int64_t dts_rstate[MAXCPU][2]; /* per-CPU random state */
}


The per-CPU core state is initialised such that each CPU core is assigned with a non-overlapping sequence of 2^64 values.
sys/cddl/contrib/opensolaris/uts/common/dtrace/dtrace.c

for (cpu_it = 1; cpu_it < NCPU; cpu_it++) {    /*    * Each CPU is assigned a 2^64 period, non-overlapping    * subsequence.    */    dtrace_xoroshiro128_plus_jump(state->dts_rstate[cpu_it-1],
      state->dts_rstate[cpu_it]);
}


The implementation of the new random() subroutine simply reads the next pseudo-random value given the CPU state:
sys/cddl/contrib/opensolaris/uts/common/dtrace/dtrace.c

case DIF_SUBR_RANDOM: {
   regs[rd] = dtrace_xoroshiro128_plus_next(
   state->dts_rstate[curcpu]);
   break;
}


The implement of the pseudo-random number generator itself is based directly on the xoroshiro128+ generator implementation from http://xoroshiro.di.unimi.it/. This code is licenced under the Creative Commons No Copyright licence.

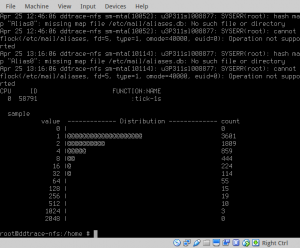
random() distribution

The new random() subroutines sampling distribution is shown below. This demonstrates a much more uniform distribution than the original LCG-base rand().

Upstreaming

In order to work towards my kernel hacking badge, improvements to dtrace’s pseudo random number generator will be considered for upstreaming in FreeBSD.

You can find out more about my work on distributed tracing on the Causal, Adaptive, Distributed, and Efficient Tracing System (CADETS) project website.

[1] https://en.wikipedia.org/wiki/Xorshift

[2] http://xoroshiro.di.unimi.it/